Rõhk vedelikes ja gaasides
Vedelikel ja gaasidel on nende siseehitusest tulenevalt üks eriline omadus – nad võivad voolata. Seepärast nimetame vedelikke ja gaase edaspidi üheskoos voolisteks.
Kui tahkele kehale mõjub rõhumisjõud, siis levib selle mõju edasi kindlas suunas – rõhumisjõu sihis.
Prantsuse teadlane Blaise Pascal tegi katsetega kindlaks, et vedelikus ja gaasis levib voolisele avaldatav rõhk igas suunas edasi ühteviisi – nimetatud lauset tuntakse seepärast ka Pascali seadusena.
Fotol on Pascali katseseade nn Pascali kera. Kliki pildil, et näha kuidas Pascali kera töötab
Seda omadust kasutatakse näiteks autode pidurisüsteemides (vaata skeemi) – avaldades piduripedaaliga torudes olevale pidurivedelikule survet, antakse see võrdselt kõikides suundades edasi rataste juures olevatele klotsidele ning kõik rattad pidurdavad ühtlaselt.
Voolise poolt temas asuvatele kehadele avaldatav rõhk
Vedeliku ja gaasi (voolise) poolt temas asuvatele kehadele avaldatav rõhk on tingitud vedelikule mõjuvast raskusjõust.
Pascal tegi katsetega kindlaks, et vedeliku poolt kehale avaldatav rõhk sõltub:
· vedelikusamba kõrgusest (mida kõrgem sammas, seda suurem on avaldatav rõhk)
· vedeliku ainest (mida tihedam on vedelik, seda suurem on avaldatav rõhk)
Vedelikusamba rõhk valemina:
Õhurõhk
Maad ümbritsevat atmosfääri saame käsitleda kui hiiglaslikku õhusammast.
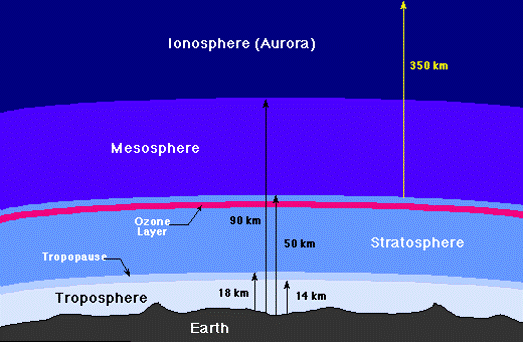
Ka atmosfääris sisalduvatele õhuosakestele mõjub Maa raskusjõud. Järelikult avaldab ka õhk temas asuvatele kehadele rõhku. Mida kõrgemale me merepinnast tõuseme, seda õhemaks jääb meie kohale jääv õhukiht – järelikult seda madalamaks muutub ka õhurõhk.
Itaalia teadlane Torricelli mõõtis ühena esimestest katseliselt ära õhurõhu (tema eksperimenti korratakse videos).
Normaalrõhuks loetaksegi Torricelli katses mõõdetud õhurõhku, mis vastab 760 mm kõrguse elavhõbeda samba poolt avaldatavale rõhule (kirjutatakse 760 mmHg)
Kuna elavhõbeda tihedus on 13 600 kg/m3, samba kõrgus 760 mm = 0,76m ning g=9,81 N/kg, saame leida normaalõhu põhiühikutes – paskalites:
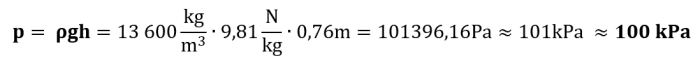
Manomeeter. Baromeeter
Manomeeter ja baromeeter on mõlemad seadeldised rõhu mõõtmiseks.
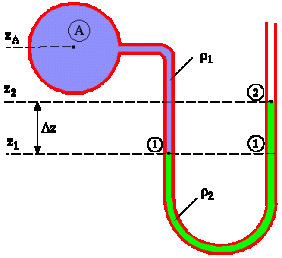Kõige lihtsam manomeeter – U-manomeeter – koosneb U-kujulisest mõõteskaalale kinnitatud torust, millesse on valatud värvitud vedelik, andurist – õhuga täidetud karbikesest, millele saab mõjuda rõhumisjõud – ning ühte toru haru anduriga ühendavast voolikust.
Kui karbikesele ei mõju jõudu, siis on vedelikunivood mõlemas U-toru osas ühekõrgused. Kui karbikesele mõjub aga rõhumisjõud, siis antakse see mööda voolikut edasi U-kujulises torus oleva vedeliku pinnale – seal tekib ülerõhk, mis surub vedelikule ning osa vedelikust surutakse toru teise osasse. Tänu sellele, et tekib vedelikunivoode erinevus, tasakaalustab kõrgem vedelikusammas ülerõhu.
Baromeeter on manomeeter, mis on kohandatud õhurõhu ja selle muutuste mõõtmiseks. Lihtsaim aneroidbaromeeter koosneb õhutihedalt suletud metallkarbikesest. Normaaltingimustes on rõhk karbis võrdne atmosfäärirõhuga. Karbikesega on ühendatud süsteem, mis registreerib karbis tekkivad pinged, mis kaasnevad välisrõhu muutusega. Kui välisrõhk suureneb, tõmbub karbike kokku, kui nõrgeneb, siis paisub.
Üleslükkejõud. Archimedese seadus
Vedeliku või gaas (voolis) avaldab sellesse asetatud kehale rõhku. Paneme tähele, et voolise rõhk keha erinevatele osadele on erinev.
Kuna keha külgpinnad asuvad voolises ühe kõrgusel ja neile mõjuvad sama suurusega rõhumisjõud (F2 ja F3) on vastassuunalised, siis tasakaalustavad külgpindadele mõjuvad jõud teineteist (R1=F2-F3=0).
Seda ei saa aga öelda keha ülemisele ja alumisele pinnale mõjuvate rõhumisjõudude (F1 ja F4) kohta. Kuna ülemise pinna kohale jääv vedelikusammas on madalam, siis on väiksem ka tema poolt avaldatav rõhk – järelikult on väiksem ka vastav rõhumisjõud. Alumisele pinnale mõjub suurem rõhk ning sellele mõjub järelikult ka suurem rõhumisjõud.
Voolises asuva keha ülemise ja alumise pinnale mõjuvate rõhumisjõudude erinevusest tekkivat resultantjõudu (R2), mis on alati suunatud vedeliku pinna poole nimetataksegi üleslükkejõuks.
Voolises asuvale kehale mõjuv üleslükkejõud on võrdeline:
- voolise tihedusega – mida tihedam vedelik või gaas, seda suurem üleslükkejõud temasse asetatud kehale mõjub
- voolisesse sukeldatud keha ruumalaga – suurema ruumalaga kehale mõjub suurem üleslükkejõud.
ehk valemina:
kus ρ – vedeliku/gaasi tihedus, mõõdetakse kilogrammides-kuupmeetri kohta (1kg/m³), g = 9,81 N/kg ≈ 10 N/kg – raskusjõu tegur Maal ja V– sukeldunud keha või selle osa ruumala mõõdetuna kuupmeetrites (1m³).
Paneme tähele, et üleslükkejõu avaldises sisalduv tiheduse ja ruumala korrutis on võrdne vastava ruumalaga voolise massiga:
Kui seda korrutada g-teguriga, on tulemuseks sellele voolise kogusele mõjuv raskusjõud.
Seega võime öelda, et voolises asuvale kehale mõjuv üleslükkejõud on võrdne tema poolt tõrjutud (temaga võrdse ruumalaga) vedelikule mõjuva raskusjõuga. Viimast lauset tuntaksegi Archimedese seadusena.
Kehade ujumine
Voolisesse asetatud kehadele mõjub lisaks üleslükkejõule alati ka raskusjõud. Kui kehale mõjub samaaegselt mitu jõudu, nende mõjud liituvad ning keha hakkab liikuma resultantjõu suunas.
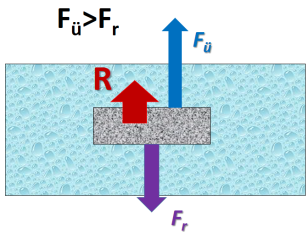
Kui üleslükkejõu ja raskusjõu resultant on suunatud voolise pinna suunas (üleslükkejõud on tugevam kui raskusjõud), tõuseb keha pinnale. Sellisel juhul öeldakse, et keha ujub vedelikus.
Kui üleslükkejõu ja raskusjõu resultant on suunatud Maa keskpunkti suunas (üleslükkejõud on nõrgem kui raskusjõud), vajub keha põhja. Sellisel juhul öeldakse, et keha upub vedelikus.
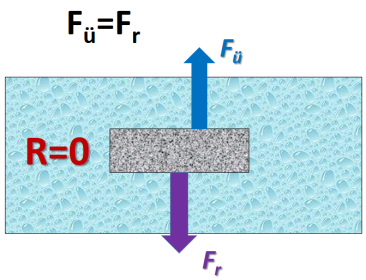
Kui üleslükkejõu ja raskusjõu resultant on võrdne nulliga – jõud tasakaalustavad teineteist, siis võib keha asetseda vedelikus ükskõik kus kohas – ta ei tõuse pinnale ega vaju ka põhja. Sellisel juhul öeldakse, et keha hõljub vedelikus.
Kuna kehale mõjuv raskusjõud sõltub keha massist (m), mis omakorda avaldub keha ruumala (V) ja keha tiheduse (ρkeha) korrutisena
Üleslükkejõudu saab aga arvutada keha ruumala (V) ja ümbritseva voolise (ρvoolis) tiheduse kaudu:
Tasakaaluolekus:
Seega keha hõljub voolises, kui keha materjali tihedus on võrdne teda ümbritseva voolise tihedusega.
Analoogiliselt arutledes jõuame järeldusele, et keha upub, kui tema tihedus on suurem kui voolise oma ning ujub kui voolise tihedus on keha tihedusest suurem.
Areomeeter
Kehade ujumistingimustel põhineb vooliste tiheduse mõõtmiseks kasutatava seadeldise – areomeetri töötamine.
Areomeeter on mingi kindla ruumalaga (enamasti klaasist ampull) keha, mille sisse on asetatud erineval hulgal raskusi (peenikesi tinakuule vms). Areomeetri mõõteskaala asub tema pikaks venitatud kaelal.
Mida tihedam on voolis, mida mõõdetakse, seda suurem on areomeetrile mõjuv üleslükkejõud ning seda rohkem tema mõõteskaala voolisest välja ulatub. Väiksema tihedusega voolistes mõjub areomeetrile väiksem üleslükkejõud ning seetõttu on ka skaala sügavamale voolisesse sukeldunud.
Kui skaala sukeldub liiga sügavale voolisesse, tuleb kasutada sama suure ruumalaga, aga väiksema massiga – see tähendab väiksema tihedusega areomeetrit. Kui areomeeter tõuseb liiga kõrgelt vedelikust välja, tuleb kasutada areomeetrit, mille mass on sama ruumala juures suurem – tihedus on suurem.
Füüsika põhivara 
You must be logged in to post a comment.