Valguse kiirus
Mõõtmistega on kindlaks tehtud, et valguse kiirus erinevates keskkondades on erinev. Kõige suurem on valguse kiirus vaakumis, kus tema väärtuseks on 300 000 km/s, kõigis teistes keskkondades on valguse kiirus aga sellest aeglasem.

Seda mitu korda on valguse kiirus on läbipaistvas keskkonnas väiksem kui vaakumis iseloomustab keskkonna optiline tihedus (n). Mida suurem on keskkonna optiline tihedus, seda aeglasemalt liigub valgus võrreldes vaakumiga. Näiteks vees liigub valgus 1,33 korda aeglasemalt (225 ooo km/s) kui vaakumis, klaasis aga koguni 1,5 korda aeglasemalt (200 000 km/s).
Valguse murdumine
Kui valgus jõuab kahe keskkonna eralduspinnale, siis muudab ta seal oma levimise suunda. Kui valgus läbib lahutuspinda ja jätkab muutunud suunas levimist uues keskkonnas, nimetatakse nähtust valguse murdumiseks.

Nii nagu valguse peegeldumist, nii kirjeldatakse ka valguse murdumist järgmiste mõistetega: valguse esialgset levimissuunda kirjeldab langev kiir, muutunud levimissuunda kirjeldab murdunud kiir ning suuna muutust kirjeldatakse vastavate nurkadega. Langemisnurk on nurk, mis jääb langeva kiire ja lahutuspinna ristsirge vahele, murdumisnurk on nurk, mis jääb murdunud kiire ja pinna ristsirge vahele.
Saame näidata, et valguse levimine on pööratav – see tähendab muutes valguse levimise vastupidiseks valguskiire tee jääb samaks.
Valguse murdumise seaduspärasused
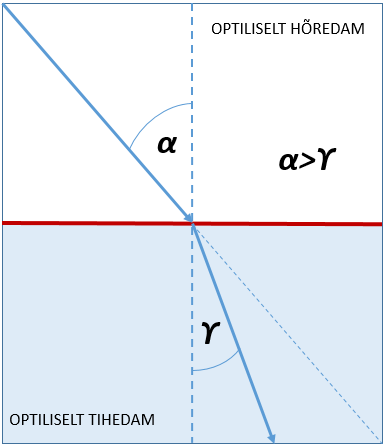
Kui valgus läheb keskkonnast, kus ta liigub kiiremini ehk tema optiline tihedus on väiksem keskkonda, kus ta liigub aeglasemalt ehk tema optiline tihedus on suurem, siis toimub valguse murdumine lahutuspinna ristsirge poole – langemisnurk on suurem kui murdumisnurk.

Kui valgus läheb keskkonnast, kus ta liigub aeglasemalt ehk tema optiline tihedus on suurem keskkonda, kus ta liigub kiiremini ehk tema optiline tihedus on väiksem, siis toimub valguse murdumine lahutuspinna ristsirgest eemale (parempoolne skeem) – langemisnurk on väiksem kui murdumisnurk.
Valguse murdumise rakendused
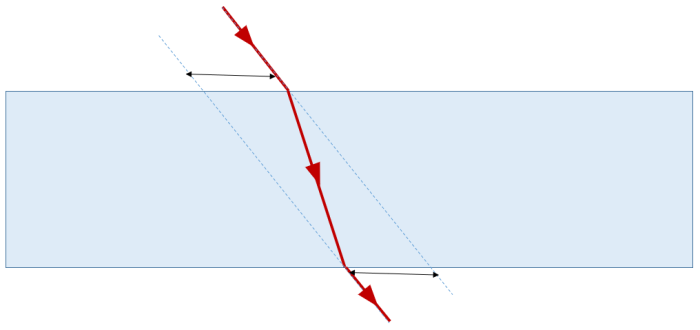
Kui valgus langeb paralleelsete tahkudega klaasplaadile, siis toimub valguse murdumine nii plaati sisenemisel kui plaadist väljumisel. Seejuures on plaati sisenenud kiir paralleelne plaadist väljunud kiirega, kuid nad on teineteise suhtes nihutatud – me näeme plaati sisenenud valgust langemas küll esialgsega samast suunast, kuid nihutatult.
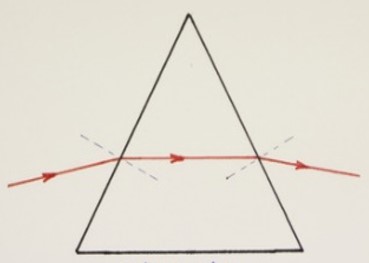
Kui valgus langeb klaasist (või muust läbipaistvast materjalist valmistatud kolmnurksele püstprismale (põhjadeks kolmnurgad, külgtahkudeks ristkülikud), siis valgus murdub nii prismasse sisenemisel kui prismast väljumisel – seetõttu näeme prismat läbinud valgust langemas esialgsega võrreldes hoopis teisest suunast.
Täielik peegeldus
Üleminekul suurema optilise tihedusega keskkonnast väiksema optilise tihedusega keskkonda, murdub valgus ristsirgest eemale. Seega peab kehtima seos, et murdumisnurk on alati suurem kui langemisnurk (kiired nr 1, 2, 3).
Murdumisnurga maksimaalne väärtus saab aga olla vaid kuni 90 kraadi (kiir nr 4), sest sellest suuremate nurkade korral (kiir nr 5) ei läbi valgus enam keskkondade lahutuspinda, vaid pöördub tagasi samasse keskkonda, kust ta pinnale langes. Taolist nähtust nimetatakse aga hoopis valguse peegeldumiseks.

Seega kui valgus tuleb läbipaistvast keskkonnast, mille optiline tihedus on suurem ja tahab minna keskkonda, mille optiline tihedus on väiksem, kuid langeb keskkondade lahutuspinnale liiga suure nurga all, ei pruugi see tal õnnestuda ning valguse murdumise asemel toimub hoopis valguse täielik peegeldumine.
Periskoobi tööpõhimõte |

Helkuri tööpõhimõte |
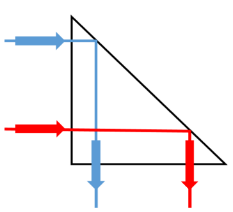
Valguse täielikku peegeldumist kasutatakse seadmetes, mille üheks (või mitmeks) komponendiks on täisnurkse kolmurgaga põhjaga püstprisma – sellel prisma tahul, millele valgus langeb tahuga risti valguse murdumist ei toimu, kuid kuna vastastahule langeb valgus kriitilisest suurema nurga all, toimub seal murdumise asemel täielik peegeldumine – valgus muudab seal (mitmekordselt) peegeldudes levimise suunda esialgsega võrreldes 90° (vasakpoolne joonis) või koguni 180° kraadi võrra (parempoolne).
Esimest omadust kasutatakse „nurga taha vaatamise“ seadeldistes – periskoopides, teist aga valgust tagasi peegeldavates helkurites.
Läätsed
Valguse murdumist kasutatakse seadeldistes, mida nimetatakse läätsedeks. Läätsed on kumerate ja nõgusate pindadega piiratud läbipaistvad kehad, mille optiline tihedus erineb ümbritseva keskkonna optilisest tihedusest.
Sõltuvalt läätse pindade kujust, liigitatakse läätsesid kumer- ja nõgusläätsedeks. Kumerläätsed on servadelt õhemad ja keskelt paksemad, nõgusläätsed aga vastupidi keskelt paksemad ja äärtelt õhemad.
|
KUMERLÄÄTSED |
||
 |
 |
 |
|
KAKSIKKUMER LÄÄTS |
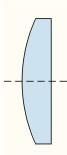
TASAKUMER LÄÄTS |
NÕGUSKUMER LÄÄTS |
|
NÕGUSLÄÄTSED |
||
 |
 |
 |
|
KAKSIKNÕGUSLÄÄTS |
TASANÕGUS LÄÄTS |
KUMERNÕGUS LÄÄTS |
 Läätsede ülesandeks on kas koondada või hajutada valgust.
Läätsede ülesandeks on kas koondada või hajutada valgust.
Kumerläätsed tavaliselt koondavad, aga nõgusläätsed hajutavad valgust. Seepärast nimetatakse kumerläätsi ka koondavateks läätsedeks, nõgusläätsi aga hajutavateks läätsedeks.
Kohta, kus koonduvat läätse läbinud murdunud kiired lõikuvad või hajutavas läätses näivad alguse saavat, nimetatakse läätse fookuseks. Fookuse kaugus läätsest – fookuskaugus – on tähtsaim läätse iseloomustav suurus.
Fookuskaugusega on seotud läätse optilise tugevuse mõiste:

kus D – läätse optiline tugevus, mõõdetuna dioptriates (1 dpt), f – läätse fookuskaugus, mõõdetuna meetrites (1m).
NB! Koondavate läätsede korral loetakse nii fookuskaugus kui sellest tulenev läätse optiline tugevus positiivseteks, hajutavate läätsede korral on nii f kui D negatiivsed.
You must be logged in to post a comment.