Mehaaniline töö
Füüsikas öeldakse, et kui keha liigub mingisuguse jõu mõjul, siis teeb see jõud keha liigutamiseks mehaanilist tööd.
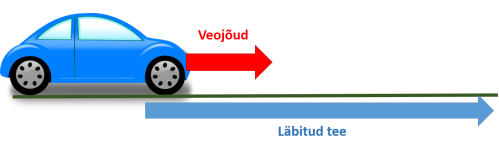
Auto läbib mootori veojõu mõjul mingisuguse teepikkuse – veojõud teeb auto liigutamiseks mehaanilist tööd.
Mehaanilise töö (A) suurus on võrdeline kehale mõjuva jõuga (F) ja keha poolt selle jõu mõjul läbitud teepikkusega (s).
kus, A- jõu poolt tehtud mehaaniline töö, mõõdetakse džaulides (1J), F – keha liigutav jõud, mõõdetakse njuutonites (1N), s – jõu mõjul selle sihis läbitud teepikkus (1m).
Töö ühik
Töö ühikuks on 1 džaul (1J). Töö ühik saadakse, kui korrutada jõu ühik (1N) pikkusühikuga (1m)
1J on selline töö, mida teeb 1N suurune jõud liigutades keha edasi 1m võrra.
Näiteks kui tõsta 100g massiga keha ühhtlase kiirusega maapinnalt 1m kõrgusele (NB! Keha liigutav jõud peab olema võrdne kehale mõjuva raskusjõuga, mis on F=mg=0,1kg×10N/kg=1N!), on tehtud töö võrdne 1J.
Võimsus
Võimsus on füüsikaline suurus, mis iseloomustab ajaühikus tehtava töö hulka.
Sisuliselt on võimsuse näol tegemist töötamise kiirust iseloomustava suurusega.
Võimsus on võrdeline tehtud tööga ja pöördvõrdeline töö tegemiseks kulunud ajaga:
kus N – jõu poolt töötamisel arendatav võimsus, mõõdetuna vattides (1W), A – jõu poolt tehtud mehaaniline töö, mõõdetuna džaulides (1J), t – töötamise aeg, mõõdetuna sekundites (1s)
Võimsuse ühik
Võimsuse ühikuks on 1 vatt (1W). Võimsuse ühik saadakse kui jagada töö ühik (1J) ajaühikuga (1s).
1 vatt on selline võimsus, kus igas sekundis tehakse tööd 1 džaul.
Näiteks kui tõsta 1 sekundiga 100g keha maapinnalt 1m kõrgusele (teha tööd 1J!), on arendatud võimsus võrdne 1W.
Energia. Mehaaniline energia
Energia on füüsikaline suurus, mis iseloomustab keha (või kehade süsteemi) võimet teha (mehaanilist) tööd.
Kui keha liigub, siis omab ta kineetilist energiat.
Kui keha on vastastikmõjus teiste kehadega, siis omavad need kehad potentsiaalset energiat.
Keha kineetilise ja potentsiaalse energia summat nimetatakse mehaaniliseks energiaks.
Kui keha energia (või mõni selle alaliikidest) muutub, siis on tehtud mehaaniline töö selle muundumise mõõduks see tähendab, et keha energia kahanemine väljendub keha poolt tehtava tööna ning keha energia kasv väljendub kehaga tehtud tööna.
Kineetiline energia
Kõik liikuvad kehad omavad kineetilist energiat
Keha kineetiline energia on võrdeline keha massiga ja ruutvõrdeline keha liikumise kiirusega:
kus Ek – keha kineetiline energia, mõõdetuna džaulides (1J), m – keha mass, mõõdetuna kilogrammides (1kg), v – keha kiirus, mõõdetuna meetrites-sekundis (1m/s).
Potentsiaalne energia
Kõik vastastikmõjus olevad kehad omavad potentsiaalset energiat.
Kui mingi keha on tõstetud Maa pinnalt mingisugusele kõrgusele, siis mõjub nende kehade vahel raskusjõud – järelikult omab maapinnalt üles tõstetud keha potentsiaalset energiat.
Maapinnalt üles tõstetud keha(le mõjuva raskusjõu) potentsiaalne energia on võrdeline keha massiga ning keha kõrgusega maapinnast:
kus, Ep – keha(le mõjuva raskusjõu) potentsiaalne energia, mõõdetuna džaulides (1J), m – keha mass, mõõdetuna kilogrammides (1kg), h – keha kõrgus maapinnast, mõõdetuna meetrites (1m) ning g =9,81N/kg ≈ 10 N/kg – raskusjõu tegur maapinnal.
Kui keha tõuseb maapinnast kõrgemale, siis tema potentsiaalne energia kasvab, kui ta liigub aga maapinnale lähemale, siis potentsiaalne energia kahaneb.
Energia jäävuse seadus
Energiat ei teki ega kao iseenesest, vaid see võib muunduda ühest liigist teise või kanduda ühelt kehalt teisele.
Selle seaduse üheks erijuhuks on mehaanilise energia jäävuse seadus: Keha mehaaniline energia on jääv juhul, kui süsteemis ei esine hõõrdumist.
Olgu keha kineetiline energia vaatluse alghetkel Ek1 ja potentsiaalne energia Ep1 ja keha kineetiline energia mingil järgneval hetkel Ek2 ja potentsiaalne energia samal hetekel Ep2.
Kui kehale ei mõju hõõrdejõudu, siis kehtib mehaanilise energia jäävuse seadus:
See tähendab, et kui mingisugusel kehal (kehade süsteemil) on mingisugusel ajahetkel mingisugune hulk (kineetilist ja/või potentsiaalset) energiat, siis on tal samasugune hulk energiat ka mistahes teisel ajahetkel. Samas kineetilise ja potentsiaalse energia hulk eraldi võetuna võib muutuda ehk nii palju kui üks energialiikidest kasvab peab teine kahanema!
Kui aga keha mehaaniline energia muutub, on see märk, et keha teeb tööd või kehaga tehakse mehaanilist tööd.
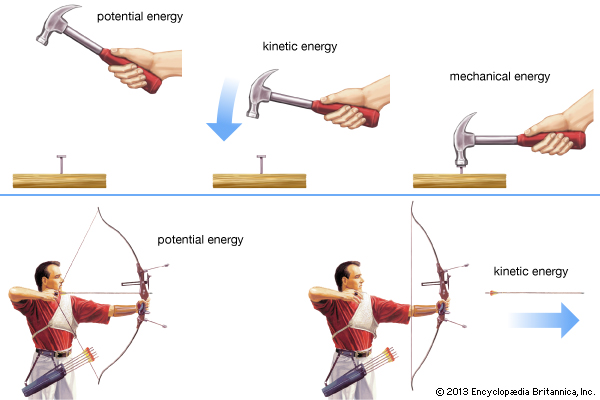
Ülemisel pildil muundub tõstetud haamri potentsiaalne energia kineetiliseks ning seejärel muundub kineetiline energia tööks, mis on tarvis teha naela lauda löömiseks. Alumisel pildil muundub pingutatud vibunööri potentsiaalne energia vibunoole kineetiliseks energiaks. Milleks võib muunduda noole kineetiline energia?
Lihtmehhanismid
Seadeldisi, mis annavad töö tegemisel võitu jõus, nimetatakse lihtmehhanismideks.
Kang
Kui mingile kehale, mis ei saa pöörelda, mõjub piisava suurusega jõud, hakkab keha selle jõu sihis liikuma.
Kui keha saab pöörelda ümber oma telje, siis hakkab keha temale mõjuva jõu mõjul hoopis pöörlema. Jõu pöörav mõju sõltub jõu suurusest, aga ka sellest, millisele kohale jõud kehas mõjub – rakenduspunktist.
Kang on mudel, mille abil saame kirjeldada jõu(dude) pööravat mõju kehadele.
Punkti, mille ümber kang pöörelda saab, nimetatakse kangi toetuspunktiks O (sest tavaliselt toetub kang selles kohas teisele kehale)
Punkte, kuhu mõjuvad kangi pööravad jõud – A ja B, nimetatakse nende jõudude rakenduspunktideks
Kaugust toetuspunktist rakenduspunktini mõõdetuna pikki kangi, nimetatakse jõu õlaks (L1 ja L2).
Kangi tasakaalutingimus
Saab näidata, et kang on tasakaalus – see tähendab, et ta ei pöörle – siis kui kangi erinevatele osadele mõjuvad jõud on pöördvõrdelised nende jõudude õlgadega:
kus F1 – kangi ühel pool toetuspunkti mõjuv jõud, d1 – jõu F1 õlg; F2 – kangi teisel pool toetuspunkti mõjuv jõud, d2 – jõu F2 õlg – jõudusid mõõdame njuutonites (1N), õlgu meetrites (1m)
Seega – mida lähemal on jõu rakenduspunkt toetuspunktile (mida lühem on jõu õlg), seda suuremat jõudu tuleb kangi tasakaalus hoidmiseks rakendada ja vastupidi – mida pikem on jõu õlg, seda nõrgemat jõudu läheb kangi tasakaalustamiseks tarvis.
Kang kui lihtmehhanism
Kang ongi kõige lihtsam lihtmehhanism – mida pikema jõu õla me kangil valime, seda väiksemat jõudu peame sellele rakendama teisel pool toetuspunkti kangi mõjutava keha liigutamiseks. Samas peame teisel pool toetuspunkti asetseva keha liigutamiseks liigutama seda otsa, millele ise jõuga mõjume palju pikema lõigu võrra.
Kangi põhimõttel töötavad ka kiiged, käärid, naelakangid jms
Pöör. Kaldpind. Kiil. Hammasülekanne
Lihtmehhanismideks, mis annavad samuti võitu jõus, on veel:
Pöör, mis koosneb vändast (hoorattast) ja võllist. Vända raadius on võlli raadiusest palju suurem – järelikult peame nööriga võlli külge kinnitatud keha liikuma panemiseks rakendama väiksemat jõudu, aga meie käed läbivad selle liigutamiseks pikema vahemaa kui võllile keritava nööri pikkus.
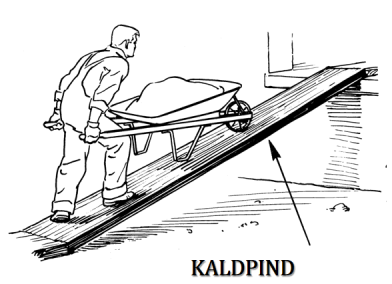
Kaldpind, mis jagab raskusjõu mitmeks komponendiks ning keha maapinnast kõrgemale liigutades tuleb kehale rakendada väiksemat jõudu, kuid keha kaldpinda mööda üles liigutades läbib keha oluliselt pikema vahemaa, kui otse teda soovitud kõrgusele tõstes.
Kiil on kaldpinna erivorm, mis on mõeldud rõhumisjõu jagamiseks mitmeks erisuunaliseks komponendiks. Seda saab kasutada kehade (näiteks küttepuude) lõhkumisel tükkideks;
Kruvi, mis koosneb ühest otsast jämedamast ja teises peenemast keermest ning milles kasutatakse asjaolu, et jämedamale otsale mõjuv pöörav jõud avaldab peenemas otsas suuremat mõju;
Plokk – mis koosneb rattakesele heidetud nöörist ning selle abil on võimalik muuta jõu mõjumise suunda – selle asemel, et tõsta raskust vertikaalselt üles, saame nööri tõmmata kaldu – taoliselt saame väiksema jõuga tõsta nööri teise otsa kinnitatud raskust.
Hammasülekanne koosneb omavahel vahetult või näiteks ketiga ühendatud hammasratastest – pöörates suuremat hammasratast mingi jõuga saavutame seeläbi väiksemale hammasrattale mõjuva suurema pöörava jõu.
Mehaanika kuldreegel
Ühegi lihtmehhanismi kasutamine ei anna meile võitu töös, sest nii mitu korda kui me võidame kehale rakendatavas jõus, kaotame selle liigutamisel teepikkuses.
Liigutades keha mööda kaldpinda üles, peame teda lükkama küll väiksema jõuga, kuid läbima selle võrra pikema tee, hammasülekande korral rakendame suuremale hammasrattale küll väiksemat jõudu, aga peame tegema mitu pööret samal ajal kui väiksem teeb vaid ühe jne.
Kasutegur
Töö, mida tehakse mehhanisme kasutamata, nimetatakse kasulikuks tööks. Kui töö tegemiseks kasutatakse mehhanisme, siis nimetatakse tehtavat tööd kogutööks. Mõõtmised näitavad, et kogutöö on alati kasulikust tööst suurem.
Kasutegur (η – eeta) iseloomustab seda, mitu korda (tavaliselt protsentides) erineb kasulik (Akasulik) töö kogutööst (Akogu).
Füüsika põhivara 
You must be logged in to post a comment.