Kujutise mõiste
Kujutis on koht, kus me näeme asuvat keha pärast seda kui temalt lähtunud valguse peegeldunud või murdunud kiired langevad meile silma.
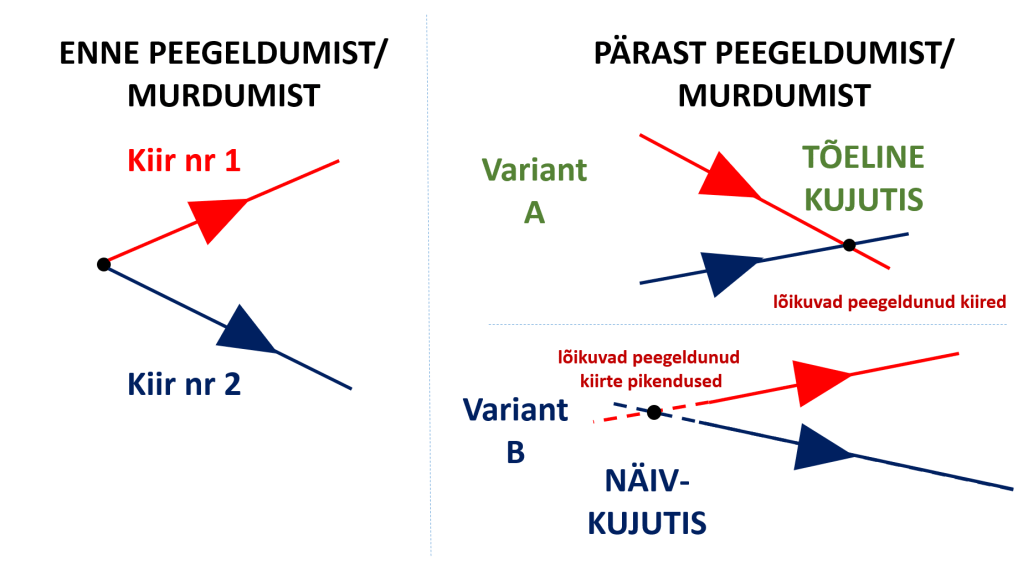
Tehnilises mõttes on tegu punktiga, kus lõikuvad peegeldunud või murdunud kiired või nende kiirte pikendused.
Kui lõikuvad murdunud/peegeldunud kiired ise, siis nimetatakse kujutist tõeliseks, kui lõikuvad kiirte pikendused, siis näiv- või ebakujutiseks.
Mõlemat tüüpi kujutist on võimalik vaadelda ja/või pildistada, kuid tõelist kujutist on lisaks sellele võimalik püüda ka ekraanile, näivat kujutist aga ekraanile püüda ei saa.
Selleks, et kirjeldada kujutiste tekkimist valguse peegeldumisel või murdumisel, peame teadma kuidas käituvad valguskiired peeglitel või valgust murdvates kehades (näiteks läätsedes)
Kujutise konstrueerimine punktist
Selleks et konstrueerida punkti kujutist – see tähendab kirjeldada punkti kujutise tekkimist peegeldumisel/ murdumisel – tuleb joonestada kahe erineva sellest punktist alguse saava kiire käigud ning leida kiirte või nende pikenduste lõikepunktid pärast seda kui kiired on peegeldunud peegelpinnal või murdunud üleminekul ühest keskkonnast teise.
Selleks et konstrueerida kujutist kehast, tuleb konstrueerida kujutis igast selle keha punktist.
Meie kasutame eseme modelleerimiseks lihtsaimat matemaatilist mudelit – sirglõiku. Selle kujutise joonestamiseks piisab kujutiste konstrueerimiseks tema mõlemast otspunktist. On lihtne näidata, et kõikide sirglõigu otspunktide vahele jäävate punktide kujutised jäävad otspunktide kujutisi ühendavale sirglõigule – sirglõigu kujutisele.
Kujutis tasapeeglis
Kujutise konstrueerimiseks tasapeeglil valime (1) üheks kiireks kiire, mis algab meid huvitavast punktist ja langeb risti peegelpinnaga ja (2) teiseks kiireks sellest punktist algava kuid peegli suhtes suvalise nurga all langeva kiire, konstrueerime nende käigud ning leiame punkti kus lõikuvad peegeldunud kiirte pikendused.
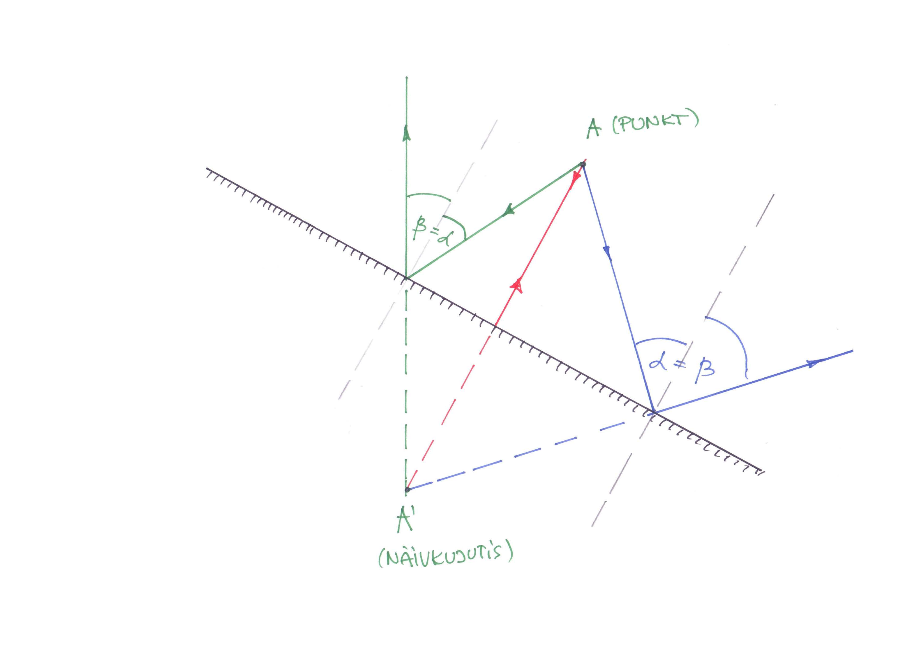
Punkti kujutise konstrueerimine tasapeeglis
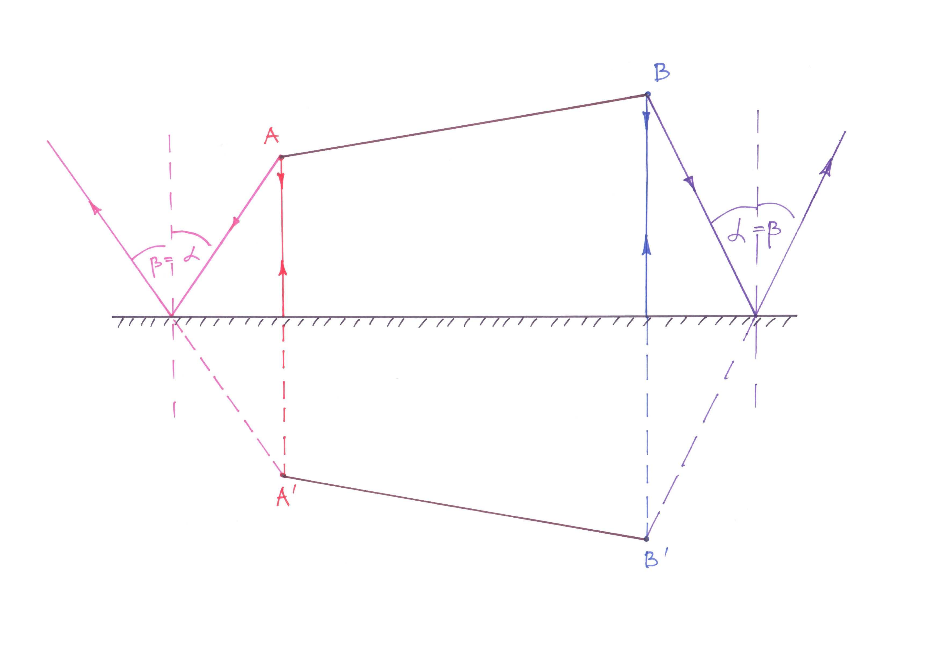
Lõigu kujutise konstrueerimine tasapeeglis
Kujutis nõguspeeglis
Kujutise konstrueerimiseks nõguspeeglil valime (1) üheks kiireks kiire, mis algab meid huvitavast punktist ja langeb risti peegelpinnaga (mööda pikendatud raadiust) ning pöördub peeglil tuldud teed pidi tagasi ja (2) teiseks kiireks sellest punktist algava ja peegli teljega paralleelse kiire, mis peegeldub ja läbib seejärel peegli fookust, konstrueerime nende käigud ning leiame punkti kus lõikuvad peegeldunud kiired või peegeldunud kiirte pikendused.
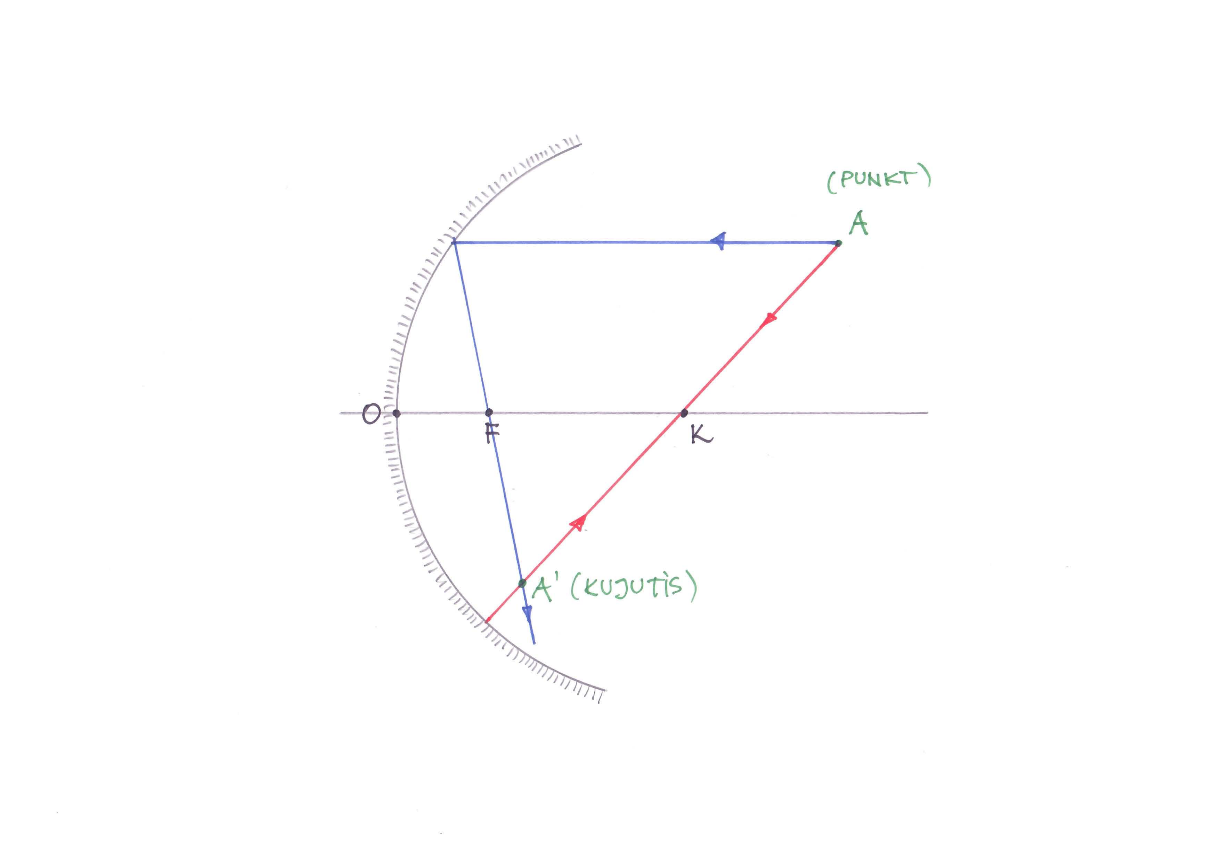
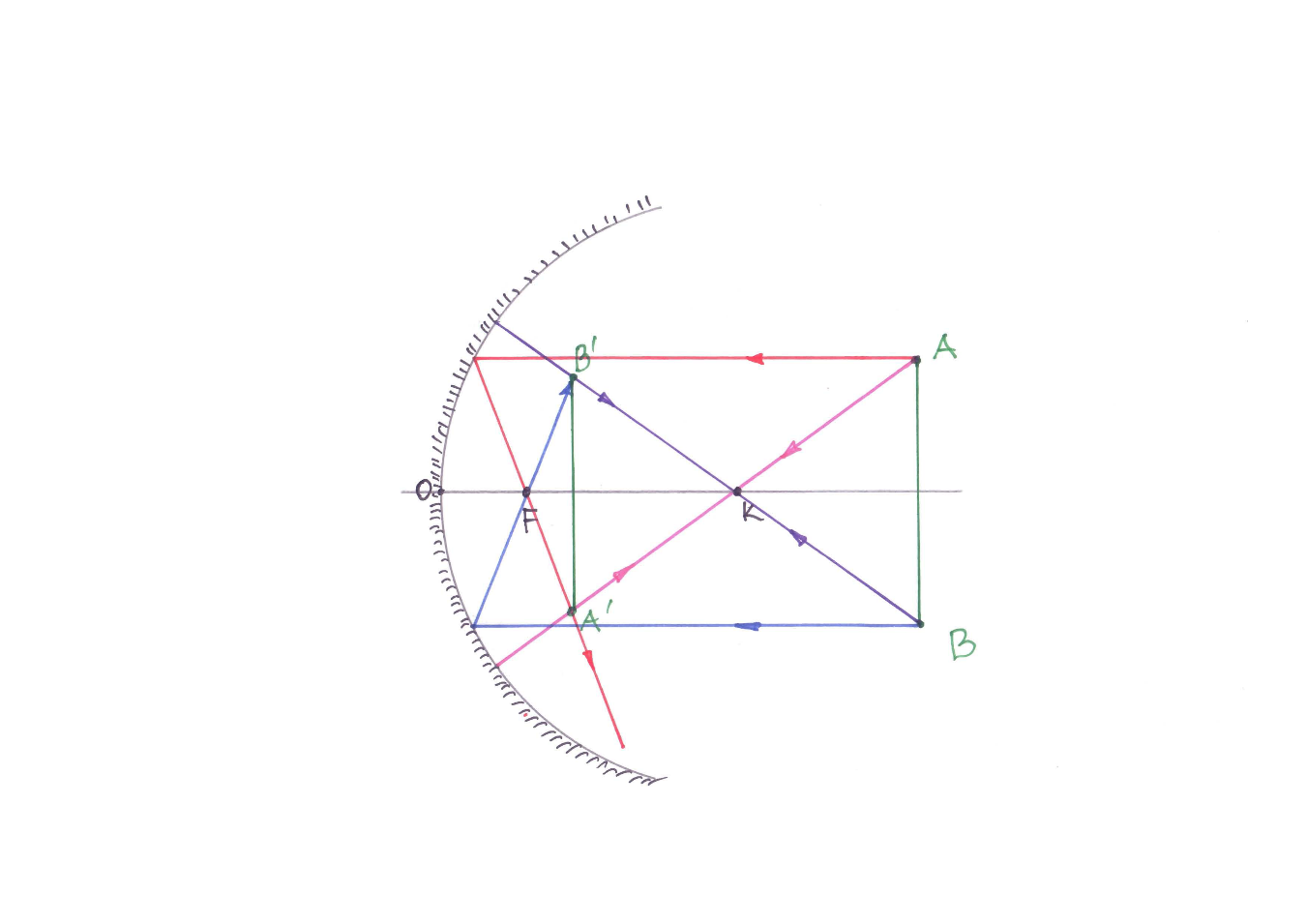
Lõigu kujutise konstrueerimine nõguspeeglis
Kujutis kumerpeeglis
Kujutise konstrueerimiseks kumerpeeglil valime (1) üheks kiireks kiire, mis algab meid huvitavast punktist ja langeb risti peegelpinnaga (mööda pikendatud raadiust) ning pöördub peeglil tuldud teed pidi tagasi ja (2) teiseks kiireks sellest punktist algava ja peegli teljega paralleelse kiire, mis peegeldub ja selle pikendus läbib seejärel peegli fookust, konstrueerime nende käigud ning leiame punkti kus lõikuvad peegeldunud kiired või peegeldunud kiirte pikendused.
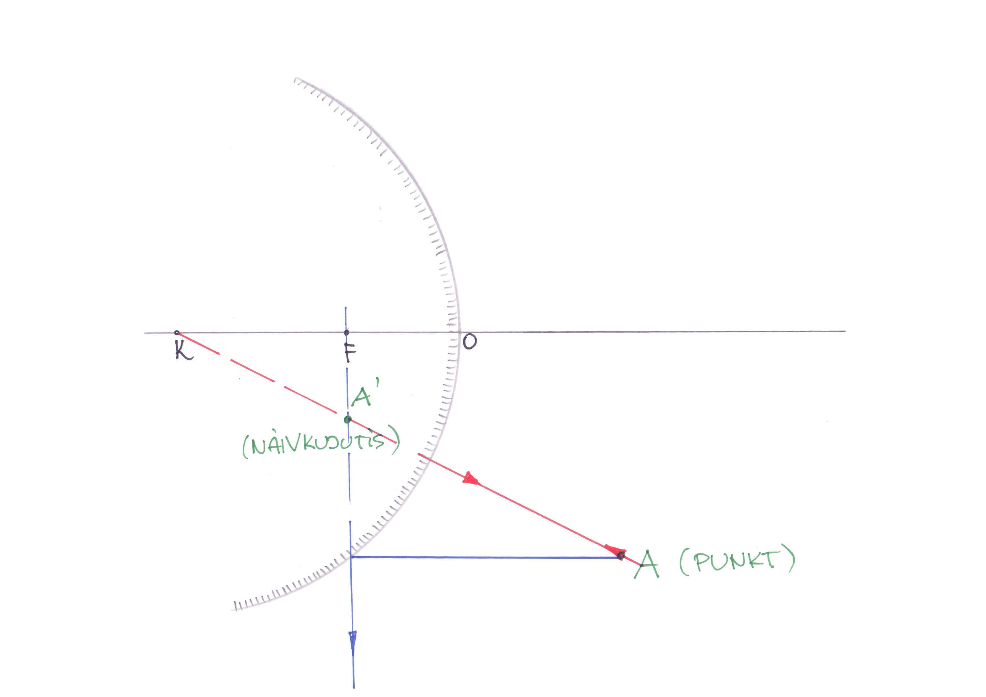
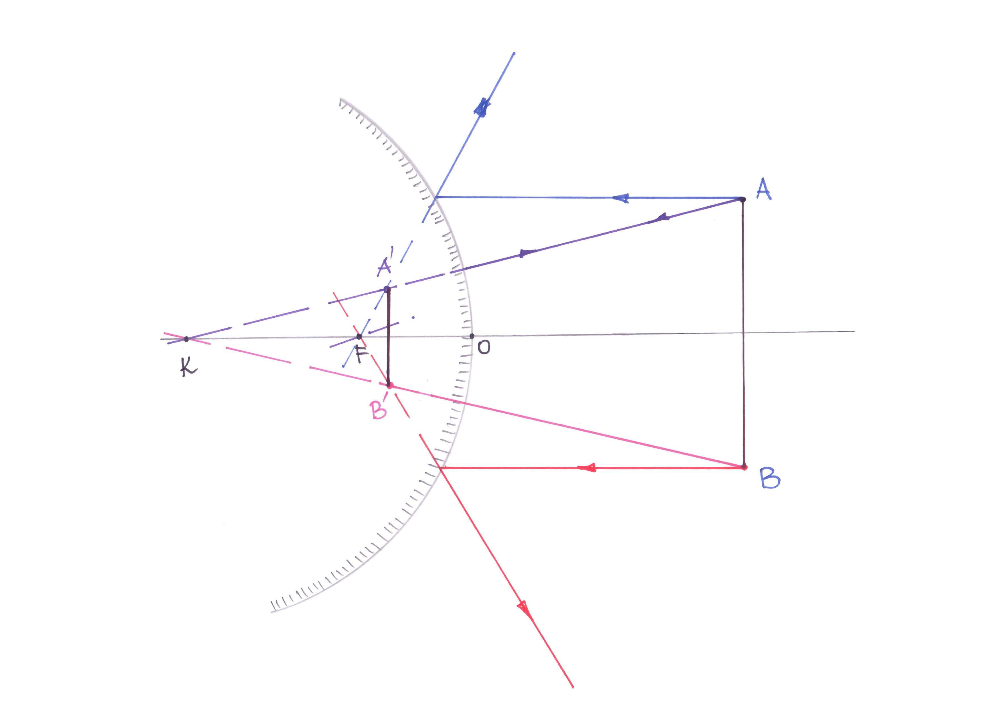
Kujutiste konstrueerimine läätsedes
Kiirte käik koondavas läätses


(2) Kiir, mis langeb läätse keskpunkti, läheb läätsest murdumata läbi
Kasutades skeemitähiseid, saame kiirte käike koondavas läätses kujutada järgmiselt:
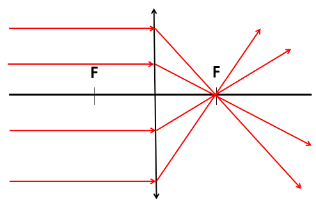
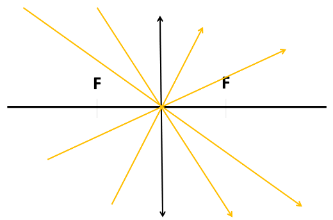
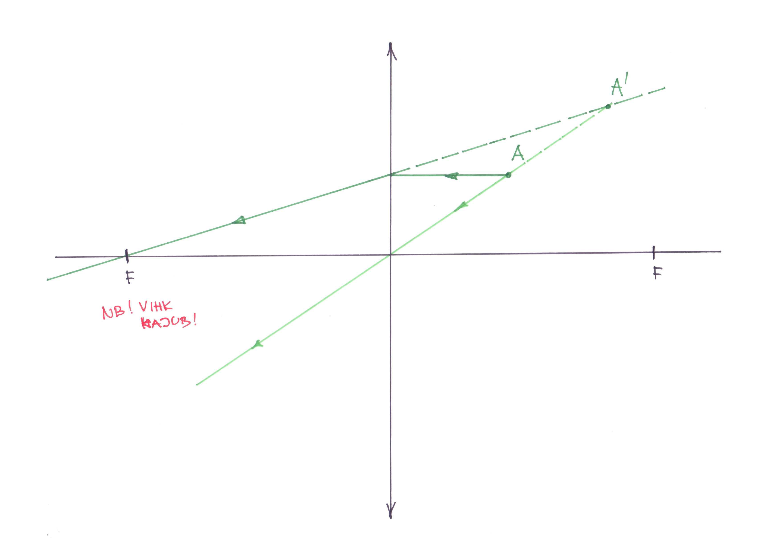
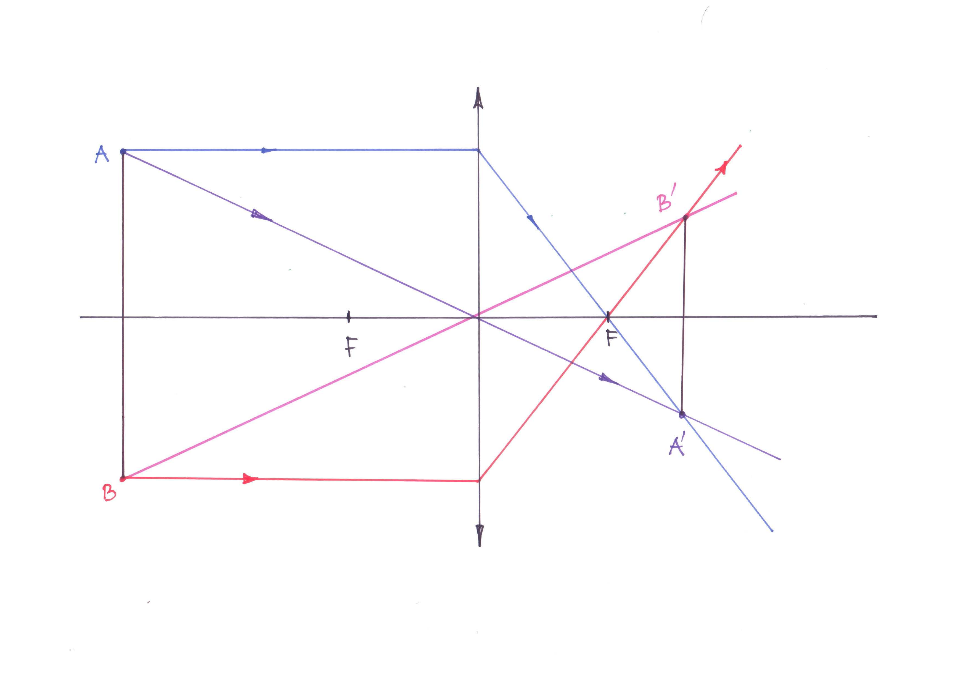
Kujutis koondavas läätses
Koondavas läätses olid lihtsalt ennustatava käiguga kiirteks
Kiirte käik hajutavas läätses


(1) Kiir, mis langeb läätsele paralleelselt optilise peateljega murdub läätse ebafookuse sihis peateljest eemale.
(2) Kiir, mis langeb läätse keskpunkti, läheb läätsest murdumata läbi
Kasutades skeemitähiseid, saame kiirte käike hajutavas läätses kujutada järgmiselt:
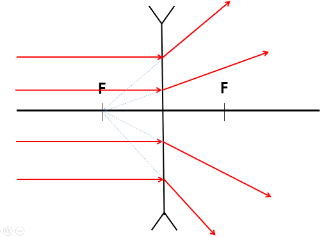
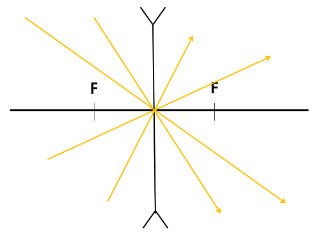
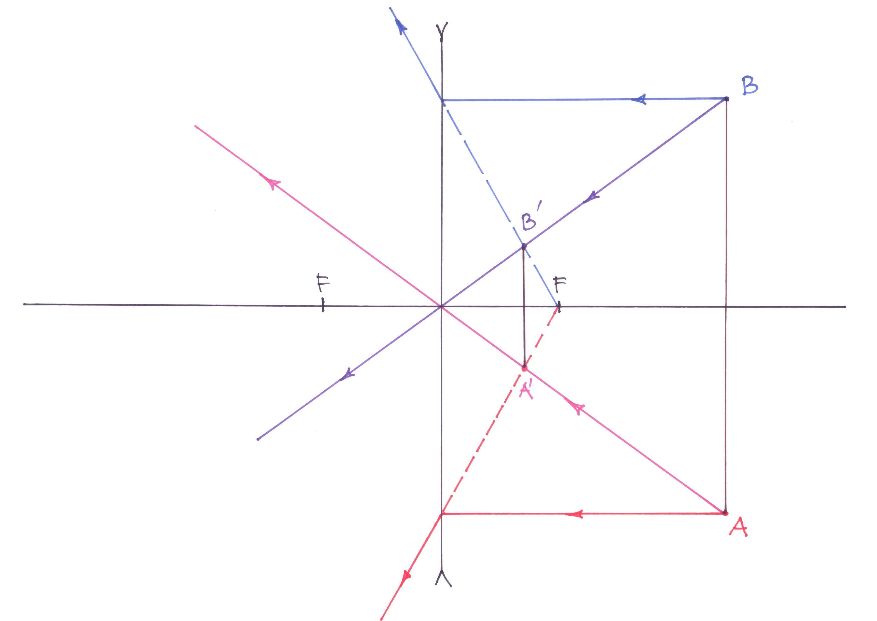
Kujutis hajutavas läätses

You must be logged in to post a comment.